LONG SHORT TERM MEMORY NETWORKS (LSTMS)

Long sequences input into an RNN will have difficulty carrying information from earlier time steps to later ones. RNNs are able to efficiently process paragraphs of text to perform predictions and they may leave out important information from the beginning, causing it to lose context. Moreover, during back propagation, RNNs suffer from the vanishing gradient problem; the network is not able to learn or improve.

LSTMs are explicitly designed to avoid the long-term dependency problem by regulating the flow of information and identifying the important information to retain and forgetting / discarding unimportant information. They are a special kind of RNN, capable of learning long-term dependencies. They were introduced by Hochreiter & Schmidhuber (1997), and were refined and popularized by many other. They work tremendously well on a large variety of problems, and are now widely used.

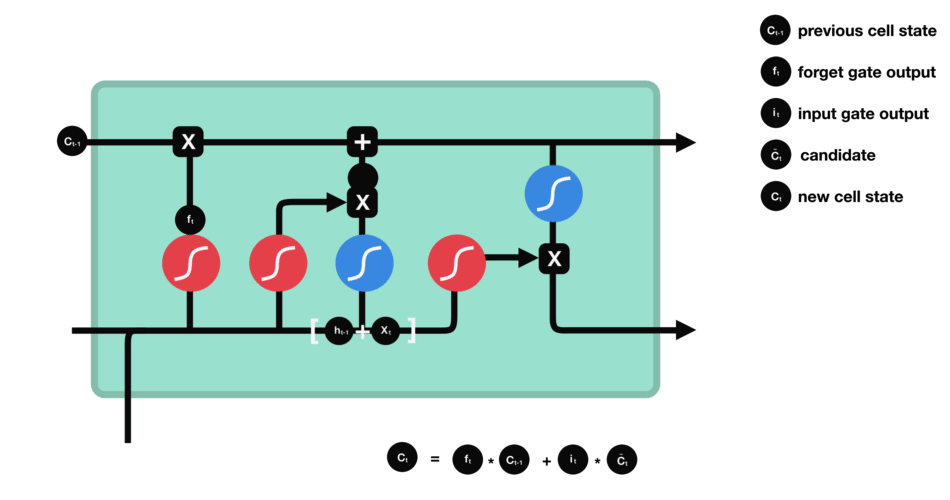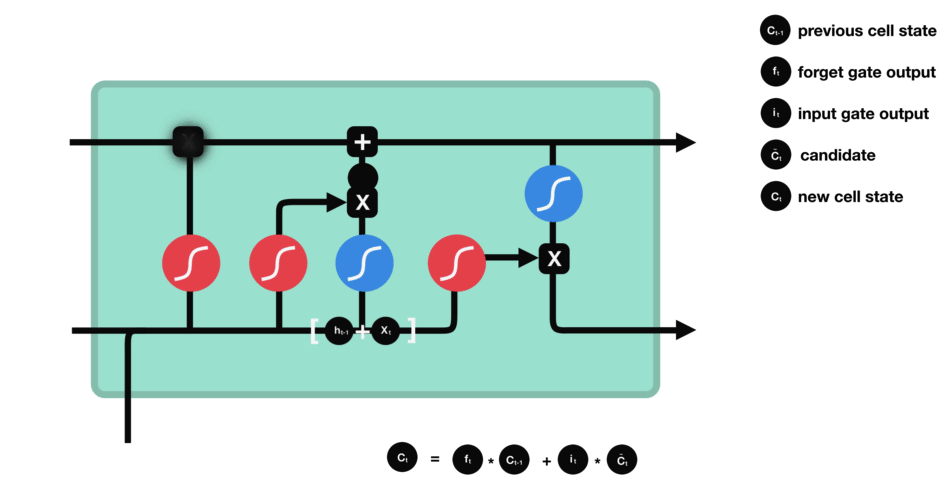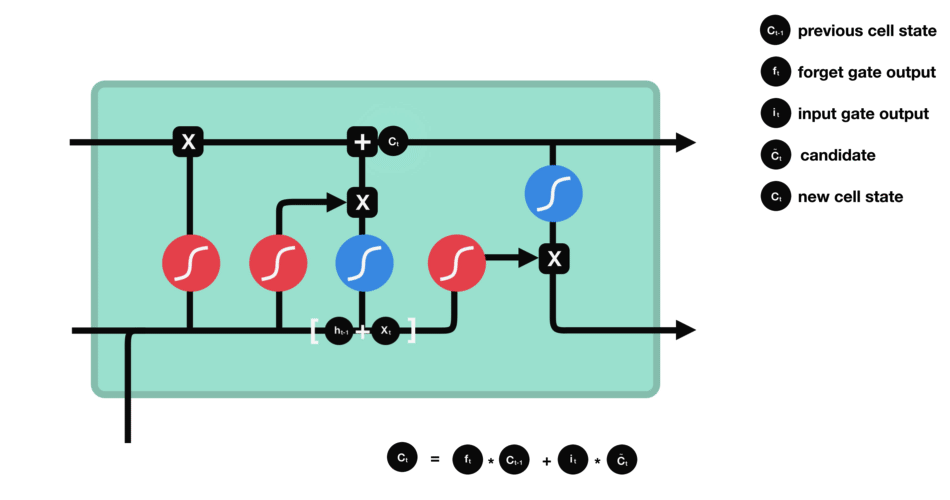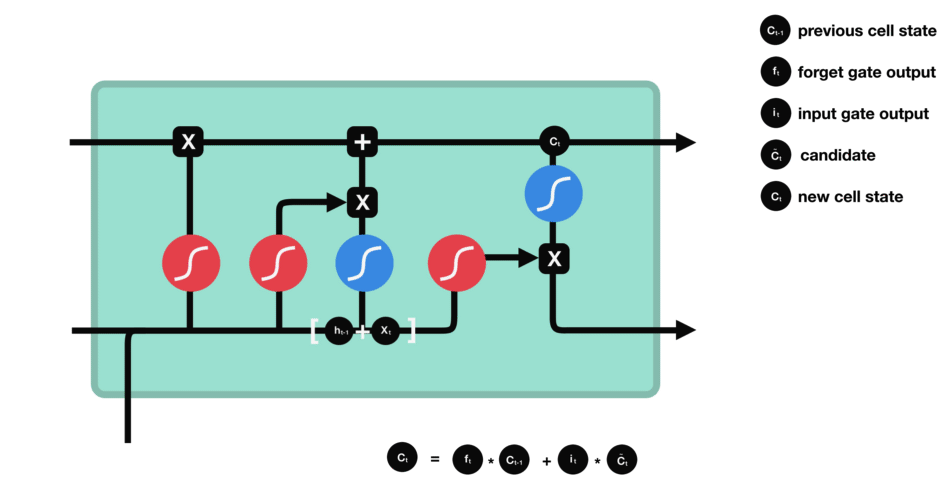
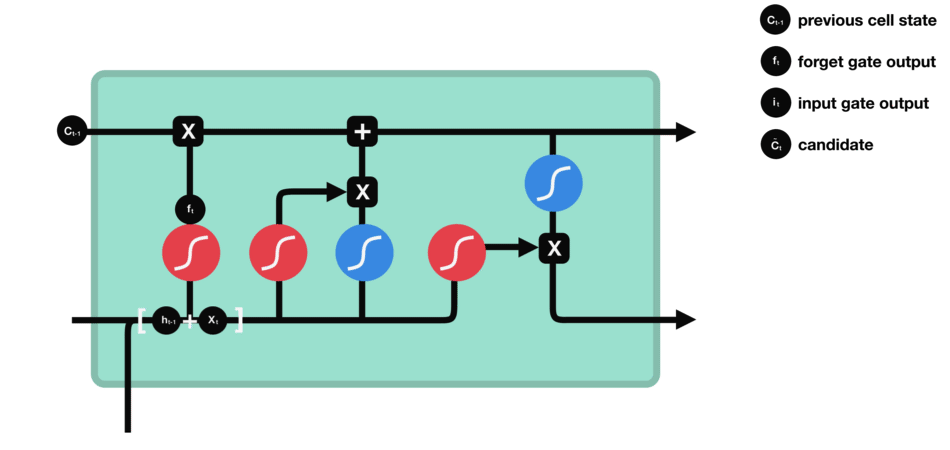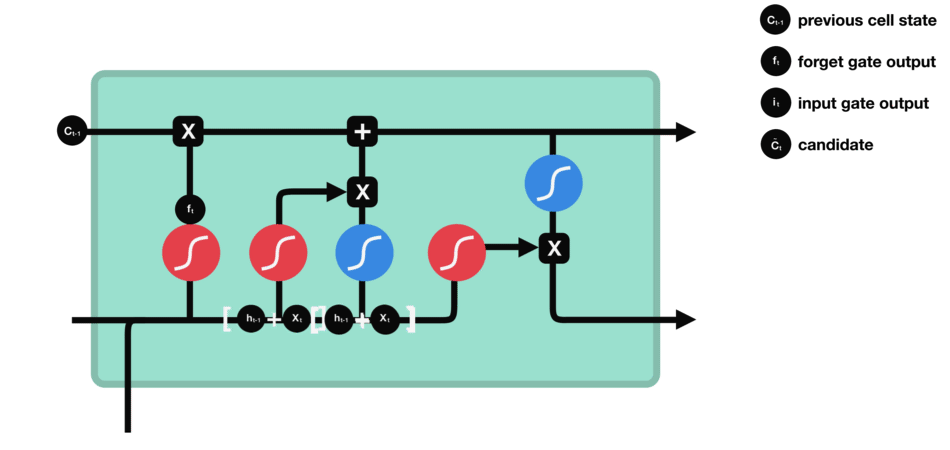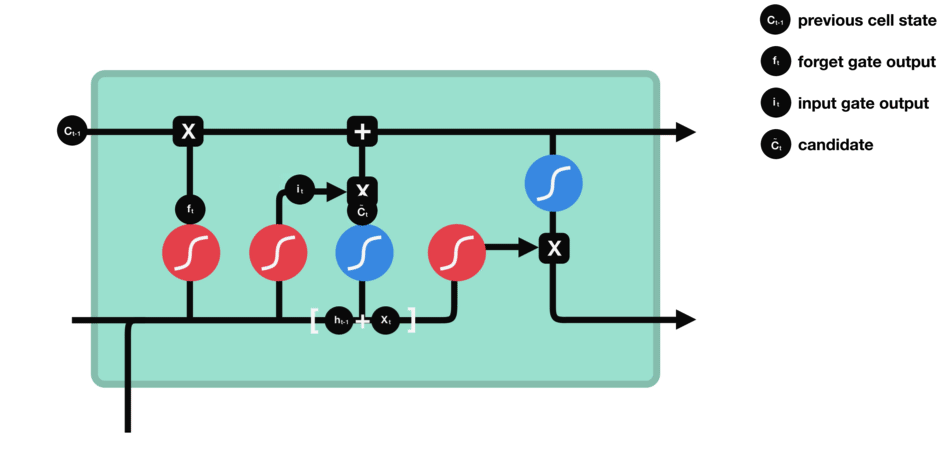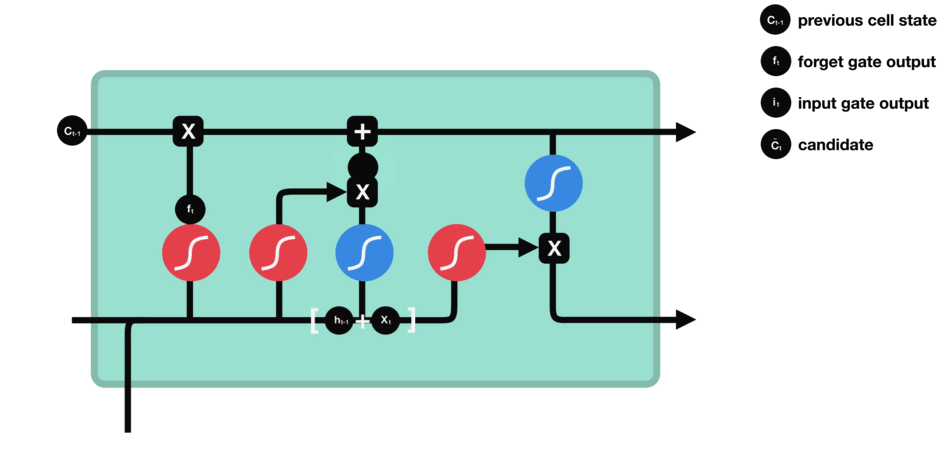
In LSTMs, the architecture of each node /cell within the hidden layers is modified to include three gates–a forget gate, an input gate, and an output gate. These gates control the flow of information within each cell to determine which information should be retained to properly predict the network output.

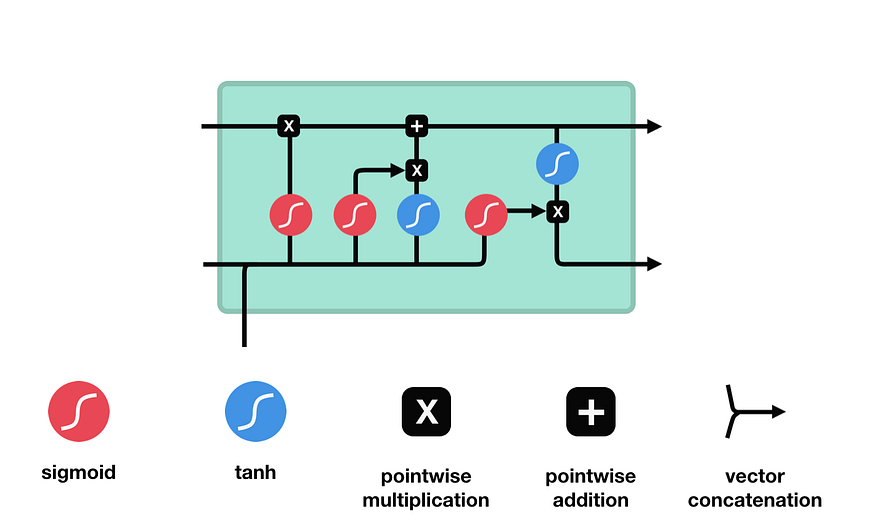
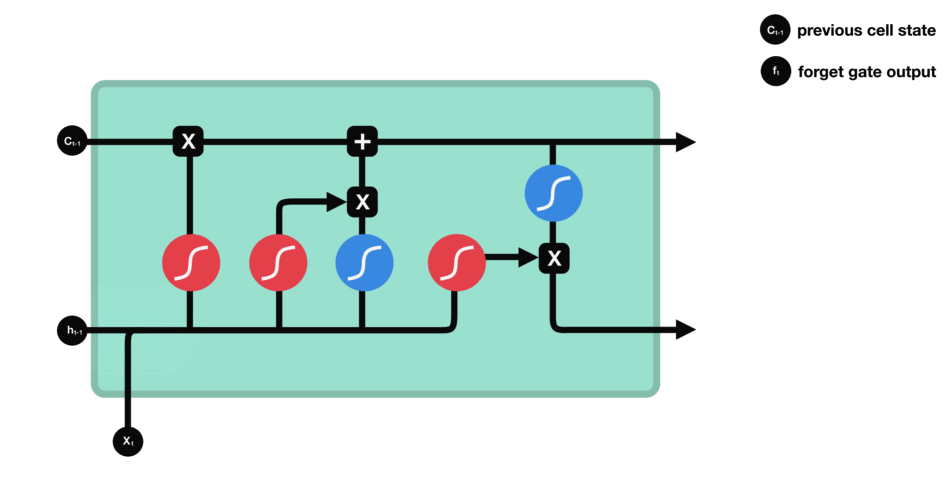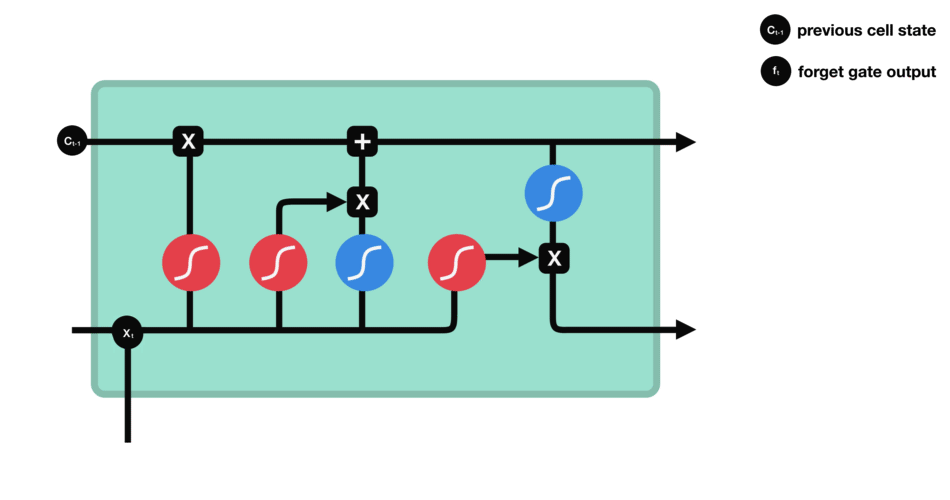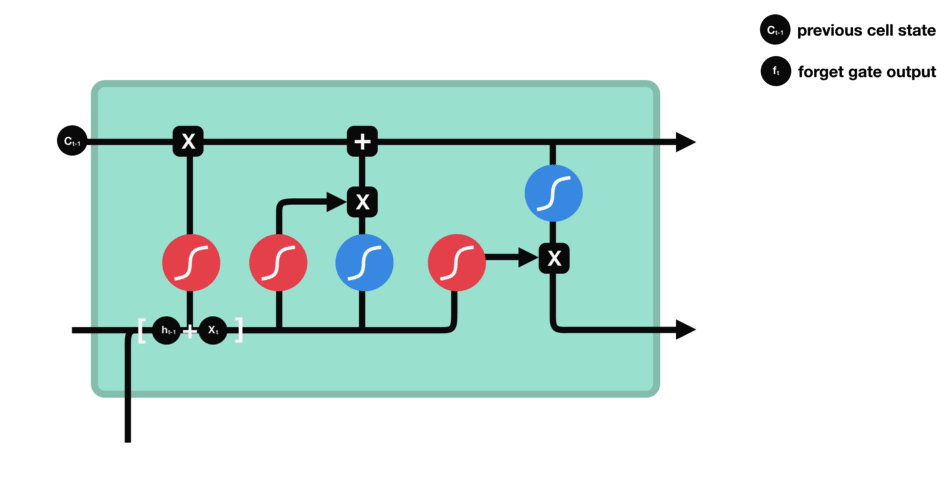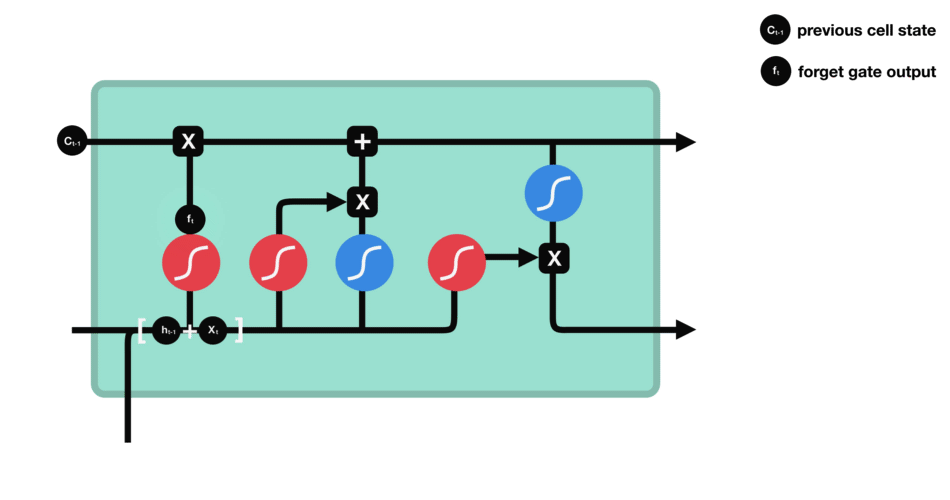
The key to LSTMs is the cell state which is indicated by the horizontal line running through the top of the diagram:

Source: TowardDataScience

The cell state runs straight down the entire chain. Gates (sigmoid calculations) are used to remove or add information to the cell state. The sigmoid outputs calculations between zero and one, enabling it to determine which information should be kept and which should be discarded. A value of zero means “let nothing through,” while a value of one means “let everything through.”

Initial Cell State

First, the cell state is determined from the output from the previous hidden layer as indicated by the top C.

Source: TowardDataScience

Forget Gate

The forget gate (first sigmoid function) determines which information will be discarded and which will be kept. Information from the previous hidden state and information from the current input (e.g., the next element of a sequence such as a word in a sentence) is passed through the sigmoid function. The calculated sigmoid values will result between 0 and 1. The closer the output is to 0, the model will discard (forget) the information. The closer the calculation is to 1, the model will retain the information.

Source: TowardDataScience

Input Gate

Next, the newly inputted information (e.g., the next element in a sequence such as a word in a sentence) is evaluated again using the sigmoid function to determine the values that will be updated. This time the input is also passed through a tanh function to create a vector of new candidate values and to squish values between -1 and 1 to help regulate the network. The output values of the sigmoid and tanh functions are multiplied to determine the new output. Similar to the previous Forget Gate, calculated values close to 0 will be discarded and values close to 1 will be retained.

Source: TowardDataScience

The product is then added to the newly updated Input State (original cell state multiplied by the forget vector) to update the cell state value to the new cell state.

Source: TowardDataScience

Output Gate

Lastly, the output gate is calculated to determine the value (vector) of the next hidden state layer. The current newly modified hidden state is passed through a tanh function and then multiplied by the sigmoid output of the current input to determine the information that will be passed to the next hidden state layer of the network. The newly modified current cell state and the new hidden information are then fed forward to the next hidden layer of the network.